[파이썬 python] Butterworth filter / low pass filter / signal data filtering

Butterworth filter 란? 

통과 대역(passband)의 진폭 스펙트럼이 아주 평평한 주파수 필터 

The Butterworth filter is a type of signal processing filter designed to have a frequency response as flat as possible in the passband. It is also referred to as a maximally flat magnitude filter. It was first described in 1930 by the British engineer and physicist Stephen Butterworth in his paper entitled "On the Theory of Filter Amplifiers".[1]

Butterworth filter - Wikipedia

통과 대역(passband) 란? 

필터를 통과 할 수 있는 주파수 또는 파장 범위 

 

Unrestricted signal (upper diagram). Bandpass filter applied to signal (middle diagram). Resulting passband signal (bottom diagram). A(f) is the frequency function of the signal or filter in arbitrary units.

 

차단 주파수 (cutoff frequency) 란?

어떤 주파수의 신호까지는 통과시키지만 그 이상(또는 그 이하)의 신호는 통과시키지 않는 기능.  

In physics and electrical engineering, a cutoff frequency, corner frequency, or break frequency is a boundary in a system's frequency response at which energy flowing through the system begins to be reduced (attenuated or reflected) rather than passing through.

 

Magnitude transfer function of a  bandpass filter  with lower 3 dB cutoff frequency  f 1  and upper 3 dB cutoff frequency  f 2

low-pass filter (LPF) 란?

선택된 cutoff frequency 보다 낮은 주파수의 신호를 통과시키는 필터

A low-pass filter (LPF) is a filter that passes signals with a frequency lower than a selected cutoff frequency and attenuates signals with frequencies higher than the cutoff frequency. The exact frequency response of the filter depends on the filter design. The filter is sometimes called a high-cut filter, or treble-cut filter in audio applications. A low-pass filter is the complement of a high-pass filter.

The Bode plot of a first-order Butterworth low-pass filter

The order of the filter determines the amount of additional attenuation for frequencies higher than the cutoff frequency.

Plot of the gain of Butterworth low-pass filters of orders 1 through 5, with  cutoff frequency   {\displaystyle \omega _{0}=1} . Note that the slope is 20 n  dB/decade where  n  is the filter order.

 

Nyquist frequency 란? (nyq)

샘플링(sampling) 법칙에 의하면 샘플링 주파수 fs는 신호의 최대주파수 성분의 2배 이상이 되어야 한다. 이는 fs/2 이상의 주파수 성문에서는 중첩(folding)현상이 발생하여 알리아싱(aliasing)현상이 발생하기 때문이며, 이때 fs/2를 중첩 주파수 또는 나이퀴스트 주파수라 부른다. 디지털 신호분석 시, 입력신호를 A/D변환기에 의하여 디지털화할 때 N개의 이산화값(discrete value)으로 기록된다. 샘플링 주파수(fs), 나이퀴스트 주파수(f0), 분해는 주파수(Δf)사이에는 다음과 같은 기본식이 성립한다. 즉, fo=fs/2, Δf=fs/N.

[네이버 지식백과] Nyquist Frequency - 나이퀴스트 주파수 (지형 공간정보체계 용어사전, 2016. 1. 3., 이강원, 손호웅)

 

Fig 1. The black dots are aliases of each other. The solid red line is an  example  of adjusting amplitude vs frequency. The dashed red lines are the corresponding paths of the aliases.

 

 

[python code]

 

기본 코드

(출처 : https://medium.com/analytics-vidhya/how-to-filter-noise-with-a-low-pass-filter-python-885223e5e9b7) 

import numpy as np
from scipy.signal import butter, filtfilt 
import matplotlib.pyplot as plt 

def butter_lowpass_filter(data, cutoff, fs, order):
	normal_cutoff = cuttoff/nyq
    b, a = butter(order, normal_cutoff, btype='low', analog=Flase)
    y=flitflit(b, a, data)
    return y 


T = #period(time interval)
fs = #rate(total number of samples/period)
cutoff = 2 #cutoff frequency

nyq= 0.5*fs
order=2 #filter order
n= int(T*fs) #total number of samples 

butter_lowpass_filter(data, cutoff, fs, order) 

 

[calcium signal analysis code] 

 

import numpy as np
from scipy.signal import butter, filtfilt 
import matplotlib.pyplot as plt 

def butter_lowpass_filter(data, cutoff, fs, order): 
	normal_cutoff=cutoff/nyq 
    b, a = butter(order, normal_cutoff, btype='low', analog=Flase)
    y=filtfilt(b, a, data)
    return y 
    
T = #time interval 
fs = #sample rate 
cutoff = 2 #sample frequency 

nyq = 0.5 * fs 
order = 2 
n = int(T*fs) #total number of samples 

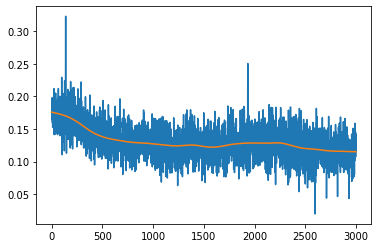
data = #raw data 

F=butter_lowpass_filter(data, cutoff, fs, order)
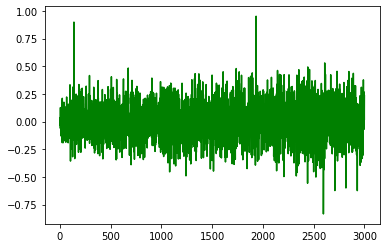
deltaF=(data-F)/F

 

blue : data (raw data), orange : F (filtered base), green : deltaF

 

 

출처 : wikipedia, NAVER 지식백과